1509. Раздел королевства

 

Король страны Геометрии в заботах. У него есть три сына, которые постоянно ссорятся. Король применял разные методы примерения, но все напрасно. И это его очень беспокоило.

“А что если разделить королевство?”, – подумал король. Он пригласил советников и описал свой план. Король открыл карту.

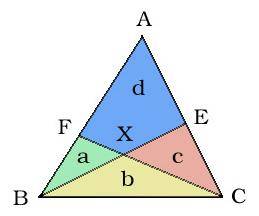
Королевство имеет форму треугольника с вершинами 'A', 'B', 'C'. Король провел линию от B к E (E - произвольная точка на отрезке AC) и линию от C к F (F - произвольная точка на отрезке AB). Пересечение BE и CF обозначено через X.

Теперь образовалось четыре части – a (треуголььник BFX), b (треуголььник BCX), c (треуголььник CEX) и d (четырехугольник AEXF). Король решил отдать области a, b, c трем сыновьям. А область d станет новым королевством.

Вы – главный советник. Король сообщает Вам значения a, b и c. Вам необходимо найти значение d. Если его найти невозможно, то сообщить об этом.

 

Вход. Состоит из не более чем 1000 тестов. Каждый тест содержит три неотрицательных действительных числа a, b, c (разделенных пробелом). Входные данные заканчиваются тестом у которого a = -1 и он не обрабатывается.

 

Выход. Для каждого теста вывести его номер, начиная с 1. В следующей строке вывести d (величина области королевства после раздела) округленное до 4 десятичных знаков или 'Poor King!' (без кавычек) если значение d определить невозможно. Формат выходных данных показан в примере.

 

Пример входа

Пример выхода

1 2 1

2 4 2

1 3 3

-1 0 0

Set 1:

2.0000

Set 2:

4.0000

Set 3:

5.0000

 

 

РЕШЕНИЕ

геометрия

 

Анализ алгоритма

Искомую площадь d будем искать как сумму площадей d1 и d2.

 

 

 

 

 

 

 

 

 

 

 

 


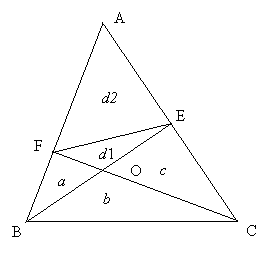
Треугольники BFO и EFO имеют общее основание FO. Следовательно их площади d1 и a относятся как высоты, опущенные из вершин E и B на прямую FO. Аналогично треугольники BCO и ECO имеют общее основание CO. Значит их площади c и b относятся как высоты, опущенные из вершин E и B на прямую CO.

То есть , откуда .

Теперь рассмотрим треугольники CAF  и CBF с основаниями AF и BF. Они имеют одинаковую высоту, опущенную из вершины С на прямую AB. Следовательно площади этих треугольников относятся как длины сторон AF и BF.

Рассмотрим треугольники EAF  и EBF с основаниями AF и BF. Они имеют одинаковую высоту, опущенную из вершины E на прямую AB. Площади этих треугольников относятся как длины сторон AF и BF.  Имеем:

,

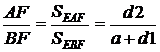
Следовательно . Поскольку d1 уже найдено, то имеем равенство с одним неизвестным d2:

, ,

,

Если , то решения не существует.

 

Реализация алгоритма

Читаем входные данные для каждого теста, вычисляем значение площади d1.

 

while(scanf("%lf %lf %lf",&a,&b,&c), a != -1.0)

{

  d1 = a * c / b;

  printf("Set %d:\n",cs++);

 

Проверяем условие b > d1 и вычисляем площадь d2. Искомая площадь d равна d1 + d2.

 

  if (b > d1)

  {

    d2 = (a + d1) * (c + d1) / (b - d1);

    printf("%.4lf\n",d1+d2);

  }

  else printf("Poor King!\n",d1+d2);

}